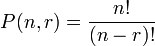Her hangi bir konuda seçim yapma işlemi hem günlük yaşantımızda hem de matematik biliminde sıkça karşılaştığımız bir durumdur. Seçim yapma durumunda kaldığımızda kaç tane seçim yapma durumunun olduğu, en iyi seçimin hangisi olduğunu bilmek isteyebiliriz. Kombinasyon bu şekilde bir grup içerisinden seçim yapmak istendiğinde kaç farklı tipte seçim yapılabileceğinin hesaplandığı durumdur. Permütaston'da ise bir dizi içerisinde ki elemanların tekrar sayısı önem arz eder.

Alt kısımda yer alan modül ile kombinasyon ve permütasyon hesaplama için istediğiniz aralıklardaki değerleri girerek "sonucu göster" butonuna basınız.

Kombinasyon Ne Demektir?

Bir grup içerisinden seçim yapılacağı zaman, kaç farklı tipte seçim yapılacağının bulunması gerektiği durumlarda kullanılmaktadır. Grup içerisinde seçim yapılırken grup elemanlarında sıraya dikkat edilmemektedir. Kombinasyon için şu tanımda yapılabilir. Elemanlardan oluşan kümede alt kümelerin olması da denilebilir. Örnekle açıklayacak olursak;

Diyelim ki a, b, c ve d elemanlarından oluşan bir gurupta a, b, c ve de bu gurubun alt kümeleri hem de kombinasyonu denilebilir.

 

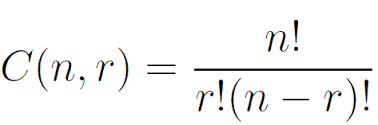
Kombinasyon Formülü

Kombinasyon bulmak için aşağıdaki formül kullanılmaktadır;

C ( n , r ) = n! / [ ( n – r )! . r!]

Kombinasyon Formülüyle İşlem Nasıl Yapılır?

Grup içerisinden seçim yapılacağı zaman kombinasyondan yani aşağıdaki formülden yararlanılmaktadır. 

Şimdi bu formülü örnekler üzerinde uygulayalım;

Örnek 1: 1,2,3,4,5 sayılarından oluşan bir grupta kaç farklı 2li kombinasyon bulunabilir.

Formülde verilenleri yerine yazarsak;

C ( 5 , 2 ) = 5! / (5 – 2 )! . 2!

=5! / 3! . 2!

= 20 / 2 = 10 farklı ikili kombinasyon bulunabilmektedir.

Örnek 2 : 8 kişinin olduğu bir grupta 6 şar kişiden kaç grup oluşturulabilir?

Verilen değerleri hemen formülde yerine yazalım;
C ( 8 , 6 ) = 8! / 2! . 6!

=56 / 2

=28 farklı grup oluşturulabilmektedir.

Örnek 3 : Bir gurupta 5 kız yer almakta. Aynı grupta 4 erkek bulunmakta. İki erkek ve iki kız seçilecek olsa kaç farklı seçim yapılabilir?

Verilen değerleri formülde yerine yazarsak;

C ( 5 , 2 ) . C ( 4 , 2 ) = [ 5! / 3! . 2!] . [ 4! / 2! . 2! ]

= 10 . 6

=60 farklı şekilde seçim yapılması mümkündür.

Permütasyon Formülü